GEOMUSIC
I view the Geomusic design like I would view something from nature. If you look at a snowflake or a leaf through a microscope you will see detailed structure that is otherwise invisible to the naked eye. The design is a sort of musical microscope giving the ability to view musical structure that is otherwise not visible. Musical structure can be heard, but the Geomusic design allows sound to be make visible and open for detailed analysis.
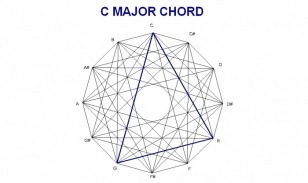
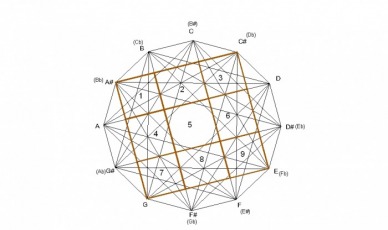
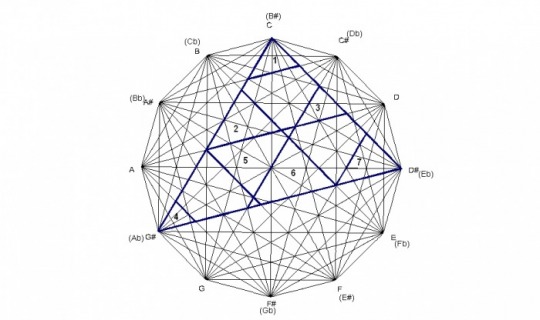
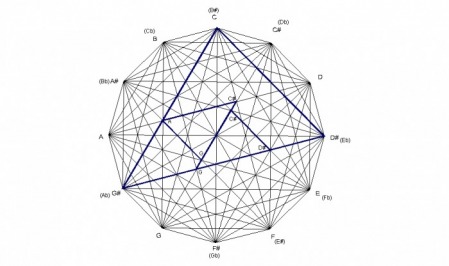
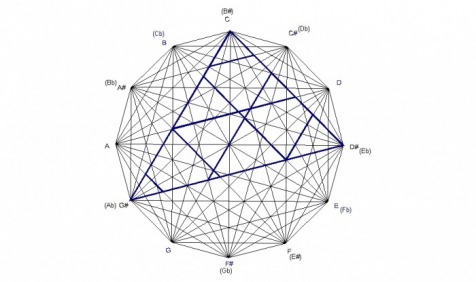
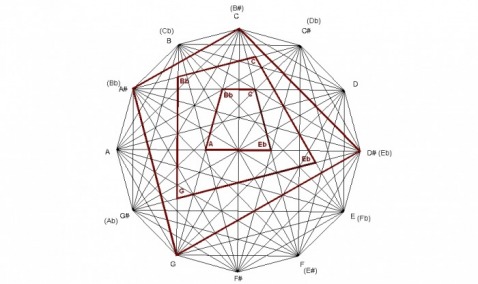
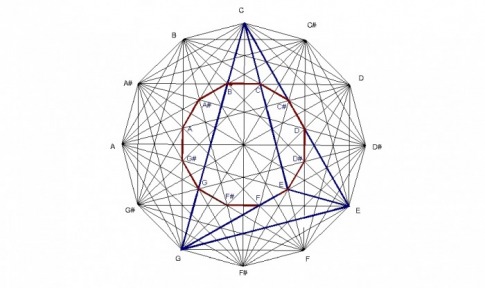
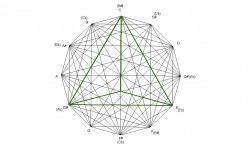
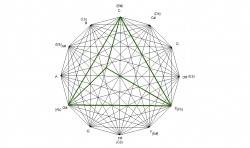
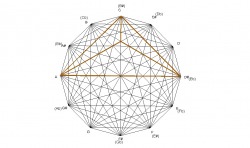
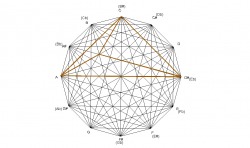
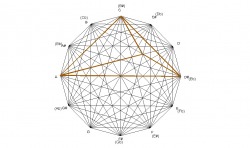
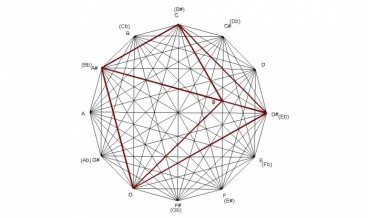
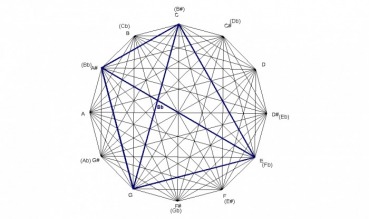
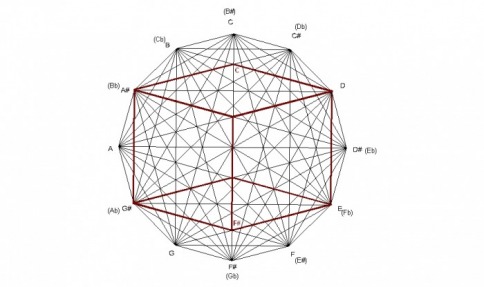
The design was created by drawing a dodecagon with sides of equal length and labeling the vertices of the dodecagon that correspond to the chromatic spacing of musical notes. The vertices are then connected corresponding to major triads forming a total of 12 triangles. Interestingly, these 12 triangles form a design that contain the four basic chord structures of western music: major, minor, diminished, and augmented, as seen in the following examples.
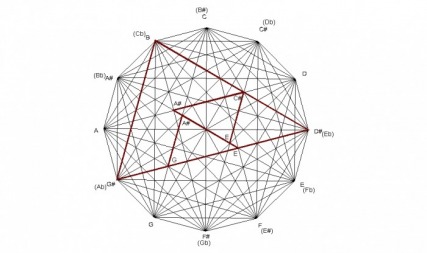
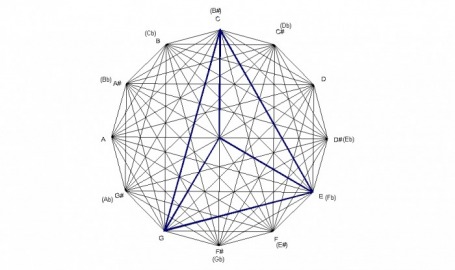
Because the design is created by major chords, any structure within the design can be analyzed to show what major chords created it. For example, the E minor chord is formed by the minor interval of the C major chord, the perfect fourth interval of the E major chord, and the major interval of the G major chord. The E minor chord is created by major chords in which the roots of each chord spell a C major chord.
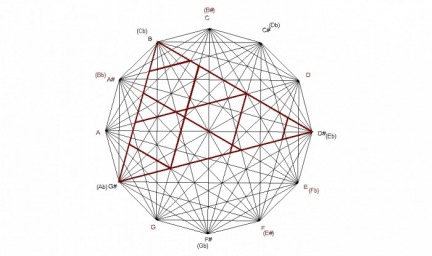
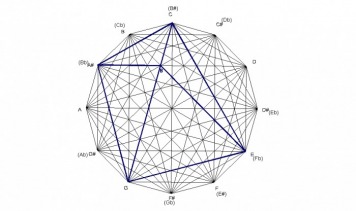
Since the design can be created by minor chords also, any structures can be explained by the minor triangles. For example, the C major chord is formed by the major interval of the A minor chord, the perfect fifth interval of the C minor chord, and the minor internal of the E minor chord. The C major chord is created by the minor chords in which the roots of each chord spells an A minor chord.
The progression here reveals a sort of organic growth pattern built on 3rds in which each chord in the progression is created by the one before. Not only does this progression sound beautiful, it cycles through each major and minor chord without the perception of a key change.
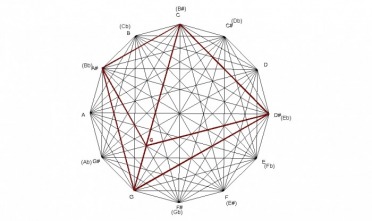
DIMINISHED CHORD
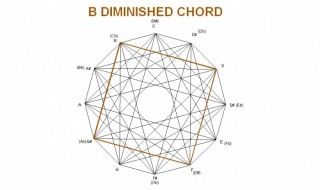
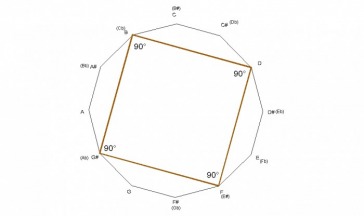
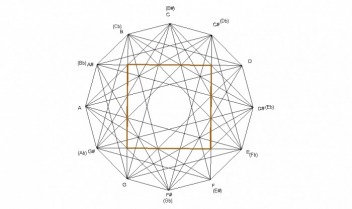
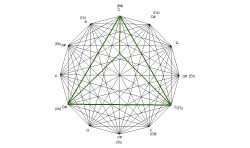
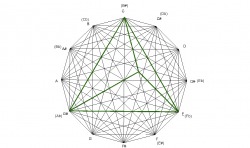
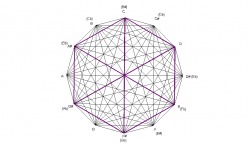
The fully diminished chord is a square as seen in the example below. Therefore, each corner has an angle of 90° . Since the fully diminished chord divides the octave in 4 equal parts, there are a total of 3 squares formed by the 3 diminished chords. The B diminished chord shown here is created by the minor intervals of the B-flat, D-flat, E, and G major chords. The roots of these chords spell a B-flat diminished chord.
Since the design can be created by minor chords also, any structures can be explained by the minor triangles. For example, the C major chord is formed by the major interval of the A minor chord, the perfect fifth interval of the C minor chord, and the minor internal of the E minor chord. The C major chord is created by the minor chords in which the roots of each chord spells an A minor chord.
The progression here reveals a sort of organic growth pattern built on 3rds in which each chord in the progression is created by the one before. Not only does this progression sound beautiful, it cycles through each major and minor chord without the perception of a key change.
DIMINISHED CHORD
The fully diminished chord is a square as seen in the example below. Therefore, each corner has an angle of 90° . Since the fully diminished chord divides the octave in 4 equal parts, there are a total of 3 squares formed by the 3 diminished chords. The B diminished chord shown here is created by the minor intervals of the B-flat, D-flat, E, and G major chords. The roots of these chords spell a B-flat diminished chord.
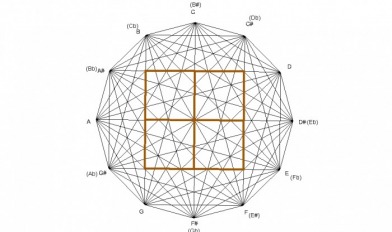
In this next example, the diminished chord is shown in its divisions of 9 quadrilaterals. Since the square is a fully diminished chord, obviously the sides of the square are formed by minor intervals while the inner lines are created by 5ths(4ths). The corner quadrilaterals(#1,3,7,9), and the center quadrilateral(#5), are perfect squares, all sided being of equal length. The center square is larger than the corner squares. The other 4 quadrilaterals(#2,4,6,8) are not squares with the line that is a part of the minor interval being longer than its two adjacent sides.
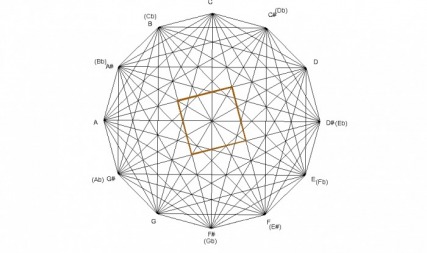
There is another square within the borders of the diminished chord at a 15° rotation. The vertices of the smaller square meet at the midpoint of the line segments of the C diminished square. Instead of the lines being created by the minor intervals, like the original diminished chord, they are created by the major intervals.
Before continuing a discussion of the diminished chord, the geomusic design, as I stated earlier, is created by major triads. This means that the tritone, and the major 2nd are not connect by line segments. These line segments are necessary at this point to show more detail within the diminished chord. Therefore, from now on, most of the examples I show will utilize the design that makes every connection between all the notes. By using the more fully developed design, some beautiful and interesting constructions are revealed. Many of these appear as three dimensional shapes which will be discussed later.
The smaller square in the last example, like the larger diminished square, can be subdivided. There are 4 squares with its inner lines created by tritones. These tritones are the diagonals of the C diminished chord; therefore the inner lines are created by notes that form the diminished chord.
The smaller square in the last example, like the larger diminished square, can be subdivided. There are 4 squares with its inner lines created by tritones. These tritones are the diagonals of the C diminished chord; therefore the inner lines are created by notes that form the diminished chord.
The final and smallest square is the middle square of the original diminished chord. The lines of this square are formed by 5ths(4ths). A diminished chord is formed by every other line. Taking the E diminished chord as an example, the middle square is formed by line segments B-G-flat, C-F, D-A, E-flat-A-flat. So there are two diminished chords: E and A.
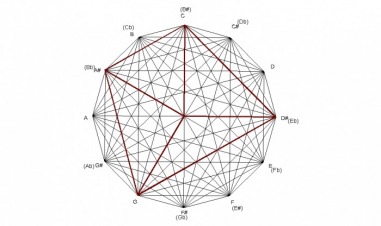
AUGMENTED CHORD
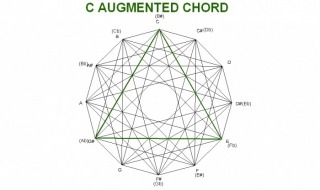
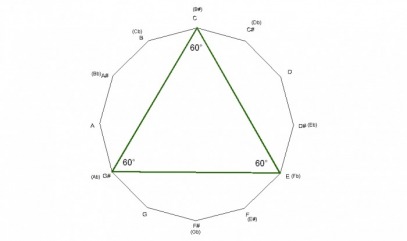
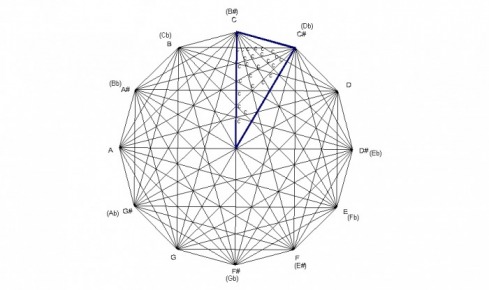
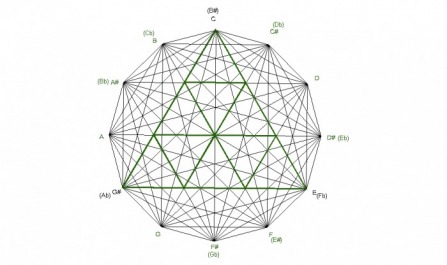
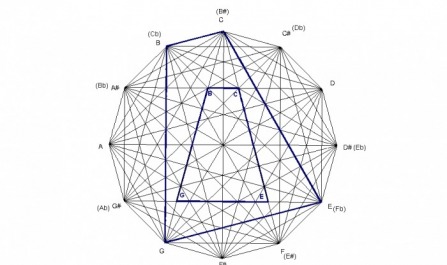
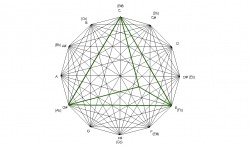
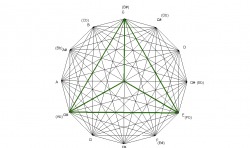
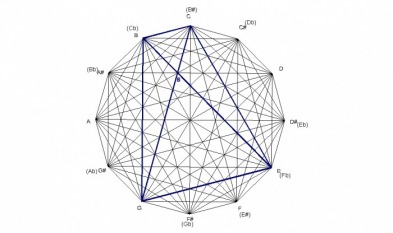
The augmented chord is an equalateral triangle which divides the octave in 3 equal parts. Since it’s an equalateral triangle, each side is of equal length, and the angles measure 60° each.
The augmented chord is an equalateral triangle which divides the octave in 3 equal parts. Since it’s an equalateral triangle, each side is of equal length, and the angles measure 60° each.
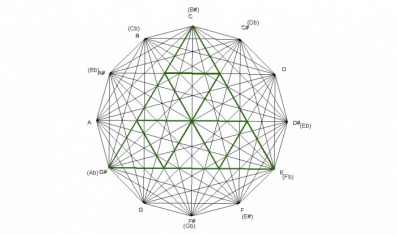
Just like the fully diminished chord, the augmented chord divides into 9 sections also. There are 9 equilateral triangles within the augmented chord. The lines that form the 9 equalateral triangles are all parallel to one of the sides of the augmented chord. The parallel lines are formed by major 3rds and tritones.
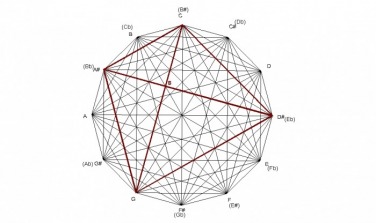
MAJOR CHORD
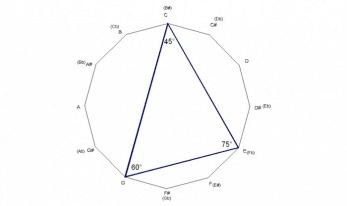
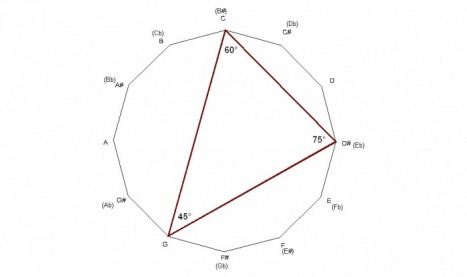
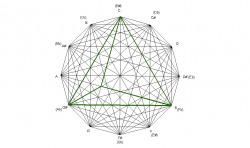
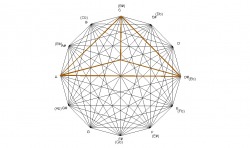
The major chord forms a triangle with angle measurements of 45° -60° -75° which means it’s an acute triangle with each angle measuring less than 90° , and it’s also a scalene triangle with all three angles having different measurements and all three sides having different lengths.
The major chord forms a triangle with angle measurements of 45° -60° -75° which means it’s an acute triangle with each angle measuring less than 90° , and it’s also a scalene triangle with all three angles having different measurements and all three sides having different lengths.
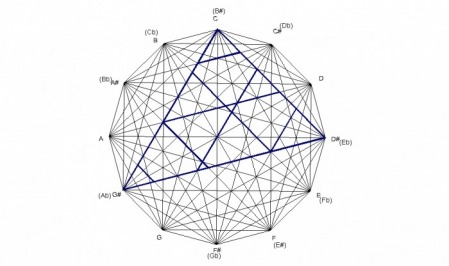
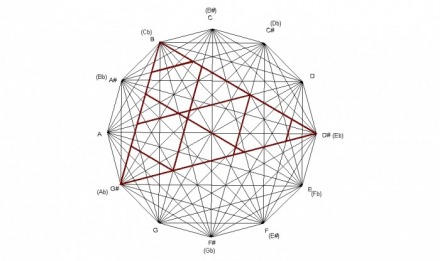
The major chord can also be subdivided into seven similar triangles. In geometry, similar triangles are defined as having congruent angles, and corresponding sides in proportion. These seven triangles are formed by 7 lines that are parallel with the sides of the major chord. In the example below of an Ab major chord, you can see two lines parallel with the 5th of the chord(Ab - Eb), two lines parallel with the major 3rd of the chord(Ab - C), and three lines parallel with minor 3rd of the chord(C - Eb).
These triangles demonstrate the theorem in geometry which states that two similar triangles can be created by drawing a line parallel to one of the sides of a triangle that intersects the other two sides.
These triangles demonstrate the theorem in geometry which states that two similar triangles can be created by drawing a line parallel to one of the sides of a triangle that intersects the other two sides.
As is demonstrated in the last example, the major chord is subdivided into 7 triangles, each with the same angles as the major chord. Three of the triangles share the Ab vertex(45° ) of the major chord, two of them share the C vertex(75° ), and two of them share the Eb vertex(60° ). The three parallel lines that form the triangles out of the Ab vertex have a minor 3rd as the shortest segment, a perfect 4th(5th) as the next larger segment, and a perfect 5th(4th) as the largest. The two parallel lines that form the triangles out of the C vertex have a minor 3rd as the smaller segment, and a 5th(4th) as the larger segment. The two parallel lines that form the triangles of the Eb vertex have a major 3rd as the shorter segment, and a tritone as the larger segment.
The major chord can also be divided into another set of 7 triangles, 3 of which are the same as the last example. Like the first 7 triangles demonstrated previously, these 7 triangles are similar to each other meaning they all have the same angle measurements as the major chord and the lengths of their sides are in proportion. These triangles are numbered in the example below.
The major chord can also be divided into another set of 7 triangles, 3 of which are the same as the last example. Like the first 7 triangles demonstrated previously, these 7 triangles are similar to each other meaning they all have the same angle measurements as the major chord and the lengths of their sides are in proportion. These triangles are numbered in the example below.
Of these 7 triangles, 3 of them have a parallel line as one of its sides, 3 of them have 2 parallel lines as its sides, and 1 of them have 3 parallel lines forming the triangle.
Also, 6 out of these triangles have their angles closest to the corresponding one on the major chord. One of the triangles, the only one that does not share the major chord as one of its sides, has the corresponding angle as the greatest distance.
There are also 2 triangles that are much smaller than the others. They too are similar triangles. They are found inside two of the other triangles. So there are 9 triangles in this set of which 7 are non overlapping.
MINOR CHORD
The minor chord triangle is congruent to the major chord triangle with angle measurements of 45° -60° -75° . The minor triangle is a mirror image of the major triangle. In other words, the major triangle could be superimposed exactly over the minor triangle but it would have to be flipped upside down to match the angles.
Also, 6 out of these triangles have their angles closest to the corresponding one on the major chord. One of the triangles, the only one that does not share the major chord as one of its sides, has the corresponding angle as the greatest distance.
There are also 2 triangles that are much smaller than the others. They too are similar triangles. They are found inside two of the other triangles. So there are 9 triangles in this set of which 7 are non overlapping.
MINOR CHORD
The minor chord triangle is congruent to the major chord triangle with angle measurements of 45° -60° -75° . The minor triangle is a mirror image of the major triangle. In other words, the major triangle could be superimposed exactly over the minor triangle but it would have to be flipped upside down to match the angles.
The minor chord is divided into the same 7 divisions as the major chord.
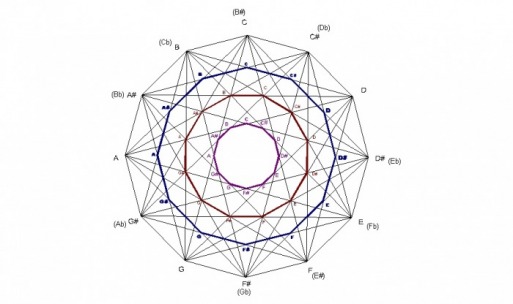
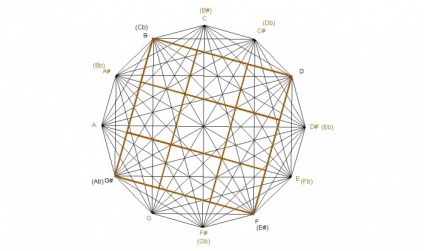
DODECAGONS
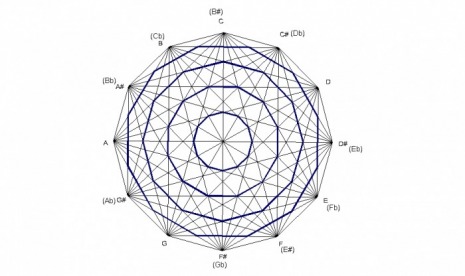
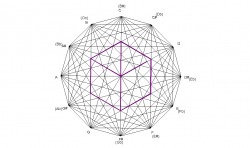
There are 4 dodecagons within the design. The smallest dodecagon is formed by 4ths(5ths), the next largest one is created by major 3rds, the next one is created by minor 3rds, and the largest by major 2nds.
There are 4 dodecagons within the design. The smallest dodecagon is formed by 4ths(5ths), the next largest one is created by major 3rds, the next one is created by minor 3rds, and the largest by major 2nds.
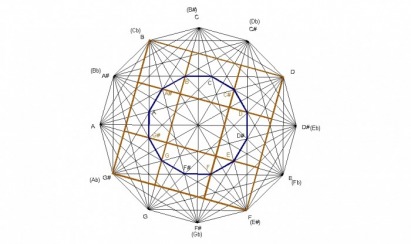
One of the questions I’ve had concerns whether individual notes can be applied to the various points within the design. I believe the dodecagons may help to answer this question. The dodecagons within the design can be viewed as smaller versions of the large dodecagon from which the design is made. Therefore, each dodecagon can be labeled with notes just like the large original one.
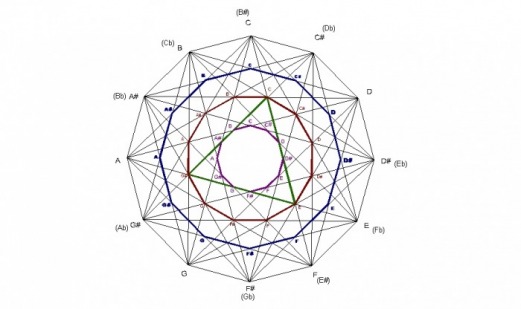
This next example seems to show the musical legitimacy of labeling the dodecagons. The green triangle connects the notes to form an augmented chord, a equilateral triangle
The second diagram shows the corresponding larger augmented triangle. Both triangles are equalateral. The smaller augmented chord is rotated 15° in relation to the larger one just like the smaller square is to the diminished chord.
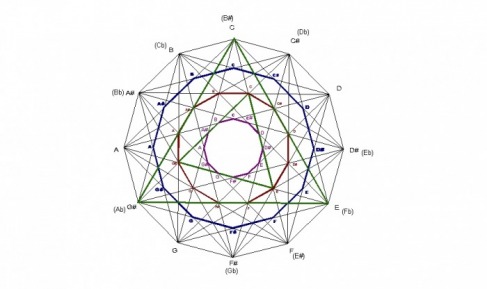
The question naturally arises whether all points of intersection can be labeled with a musical note just like the points corresponding to the dodecagons. I would suggest that that all points can be labeled when you consider the fact that each point of intersection within the design has 11 others just like it making 12 points where line segments intersect. If viewed in this way, the design can be divided into 12 congruent isosceles triangles in 30° increments. The example below shows all the line intersections corresponding to the note C. These divisions also correspond to the 4 dodecagons.
In light of labeling all the line segment intersections, I would like to analyze a couple of the triangles within the major chord. In the example below, two triangles are labeled. From the standpoint of the Ab major chord, one of the triangles is the dominant V chord(Eb - G - Bb). The other triangle is also a dominant 7th(A - C# - G) but it’s a tritone away from the other dominant chord. Notice that these two triangle form triads that have two notes in common. So the major 3rd of the Eb chord becomes the 7th of the A major chord, and the 7th becomes the 3rd.
The following example shows the corresponding triangles within the minor chord. Instead of being dominants as in the major chord, both triangles are diminished triads. Like in the major chord, these triangles share a side, and share two notes. The two diminished triads are E - G - Bb, and Bb - Db - E. Taken together, these two chords spell a fully diminished chord.
SCALES
Diminished Scales:
The parallel lines that comprise the 9 divisions of the diminished chord are based on the interval of the fifth. All of the notes that connect these parallel lines comprise a diminished scale. There is a clear connection, both geometrically and musically, between the diminished chord(square) and the diminished scale. In the example below, the notes that make up the parallel lines which form a diminished scale are colored.
Diminished Scales:
The parallel lines that comprise the 9 divisions of the diminished chord are based on the interval of the fifth. All of the notes that connect these parallel lines comprise a diminished scale. There is a clear connection, both geometrically and musically, between the diminished chord(square) and the diminished scale. In the example below, the notes that make up the parallel lines which form a diminished scale are colored.
A diminished scale is also revealed in Dodecagon 4 by the notes on this dodecagon forming a diminished scale on the paralell lines. The notes of the diminished scales are highlighted in brown.
Major Scale:
The parallel lines that comprise the 7 divisions of the major chord form a major scale. The only major scale formed by the notes that correspond to the parallel lines is a tritone away from the root of the major chord. For example, in the Ab major chord, the notes that form the parallel lines spell a D major chord. The notes of the major scale are colored.
The parallel lines that comprise the 7 divisions of the major chord form a major scale. The only major scale formed by the notes that correspond to the parallel lines is a tritone away from the root of the major chord. For example, in the Ab major chord, the notes that form the parallel lines spell a D major chord. The notes of the major scale are colored.
Minor Scale:
The same scale is formed by the 7 parallel lines within the minor chord as is formed in the major chord. The only difference is that the scale formed a tritone from the root is a minor scale.
The same scale is formed by the 7 parallel lines within the minor chord as is formed in the major chord. The only difference is that the scale formed a tritone from the root is a minor scale.
Augmented Chord:
The parallel lines that form the 9 divisions of the augmented chord form two augmented scales.
The parallel lines that form the 9 divisions of the augmented chord form two augmented scales.
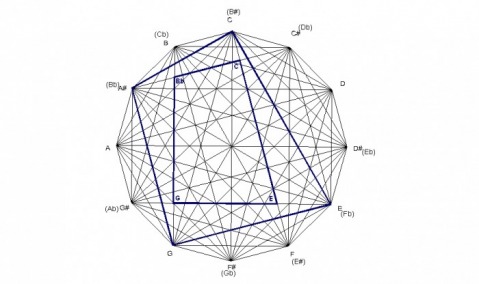
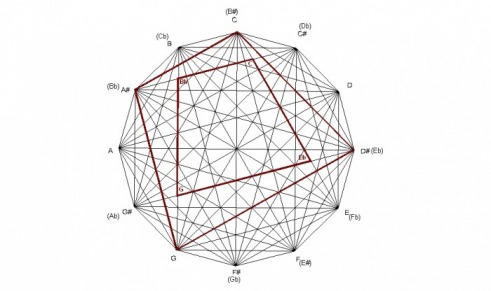
DOMINANT 7THS
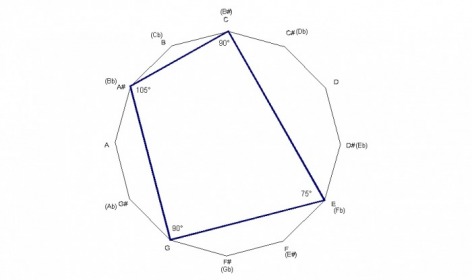
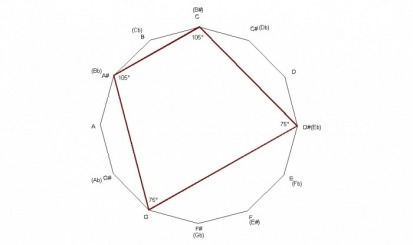
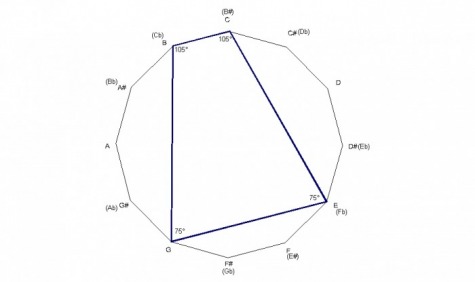
The dominant 7th chord is a quadrilateral with angle measurements of 90° -75° -90° -105° .
The dominant 7th chord is a quadrilateral with angle measurements of 90° -75° -90° -105° .
The same dominant 7th chord is found at a 15° rotation from the original one. This smaller one is similar to the larger one having the same angle measurements.
There is yet another smaller, proportional quadrilateral. However, the notes which form this quadrilateral spell a V7#9. It has the same orientation as the largest dominant chord.
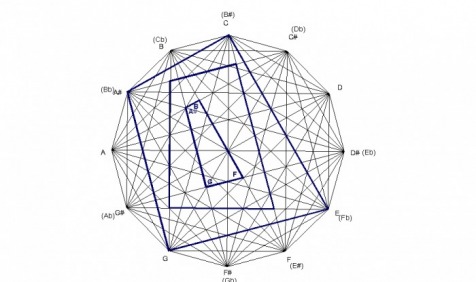
The minor 7th chord is a quadrilateral with angle measurements of 105° - 75° - 75° - 105° .
The same minor 7th chord is found at a 15° rotation from the original one. This smaller one is similar to the larger one having the same angle measurements.
There is yet another smaller, proportional quadrilateral. However, the notes which form this quadrilateral spell a Cm7#13. It is rotated 30° from the original minor 7th chord.
The major 7th chord is a quadrilateral with angle measurements of 105° - 105° - 75° - 75° , the same as the minor 7th chord.
The same major 7th chord is found at a 15° rotation from the original one. This smaller one is similar to the larger one having the same angle measurements.
THREE DIMENSIONAL SHAPES
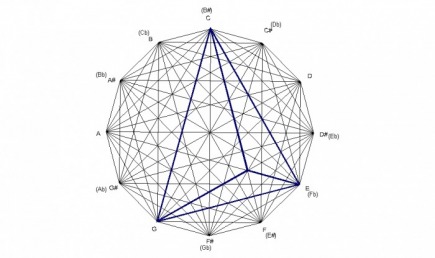
One of the most ineresting and beautiful aspects to the design is the many 3-D structures revealed throughout. In the major and minor chords there are two 3-D shapes each. These 3-D shapes are created by two types of lines, the altitude and the radius. In geometry, the altitude of a triangle is defined as a line segment that extends from one vertex and perpendicular to the opposite side. In the major and minor chords, the point at which all three altitudes intersect within the triagle is the point at which a 3-D appearance becomes evident. The following example shows the 3-D triangle based on the altitudes within a major chord.
One of the most ineresting and beautiful aspects to the design is the many 3-D structures revealed throughout. In the major and minor chords there are two 3-D shapes each. These 3-D shapes are created by two types of lines, the altitude and the radius. In geometry, the altitude of a triangle is defined as a line segment that extends from one vertex and perpendicular to the opposite side. In the major and minor chords, the point at which all three altitudes intersect within the triagle is the point at which a 3-D appearance becomes evident. The following example shows the 3-D triangle based on the altitudes within a major chord.
As can be seen in the following diagram, the point at which the three altitudes come together correspond to the note E on the highlighted dodecagon, which is the 3rd of the C major chord.
A radius is defined as the distance of a line segment from the center of a circle to a point on the circle. The radii are line segments based on trtones. The following example shows the 3-D triangle based on the radii in the major chord.
Like the major chord, the minor chord contains two 3D triangles based on the altitudes and radii.
There are a total of seven 3D Augmented Chords.
There are four 3D Half Diminished chords.
The 7th chords can be represented in 3D as seen in this C major 7th chord, which is created by connecting all of the vertices. The point of intersection of these lines corresponds with the note B, the 7th of the chord.
The minor 7th chord has a total of four 3D structures. The points of intersection spell a V chord.
The following diagram shows the dominant 7th chord in 3D. The point of intersection corresponds with the note Bb, the 7th of the chord. The second diagram is the same dominant 7th chord with the lines of intersection corresponding to the note B.
With the next diagram, we begin to see 3D structures based on scales. The following two shapes are hexagons based on the whole tone scale.
This next one is also based on the whole tone scale. Whereas the previous two whole tone cubes had inner lines based on the tritone, this one has inner lines based on four minor 3rds, four 5ths(4ths), and one tritone.
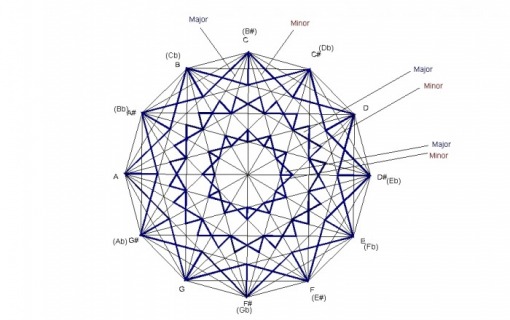
Not only can various structures within the diagram be identified by labeling the points of intersecting lines with musical notes, structures can also be identified by their angles. As seen in this diagram, there are three sets of alternating major and minor chords. The triangles labeled “major” and “minor” will correspond to the angles of the original major and minor chords from which the Geomusic design was created. The first and largest major-minor set is the same as the third and smallest set. Both of these sets have alternating major-minor triangles and the major triangles share a side with the minor triangles.
The second set is different in that the triangles do not share a side but are all connect by the vertices. Also, all three sets have a bowtie appearance but the second set is rotated 15 degrees relative to the other two sets.
The second set is different in that the triangles do not share a side but are all connect by the vertices. Also, all three sets have a bowtie appearance but the second set is rotated 15 degrees relative to the other two sets.
Another thing to note is the connection between these triangle sets and the dodecagons. Each triangle has one of its vertices connected to one of the vertices of the dodecagons. The first and third triangle sets connects to their respective dodecagon at the 75 degree angle of each triangle. The second set of triangles connects to the dodecagon at the 45 degree angle of each triangle.
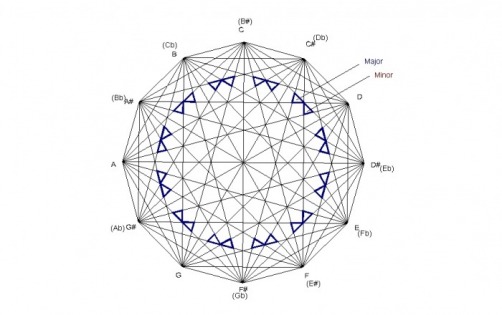
In this next example, you have another set of alternating major-minor chords. This one occurs between the first and second set contained in the previous example. It is similar to the second set in that the major triangles are connected to the minor triangles by their vertices. This set of triangles differ from the other three in that the vertices of the major-minor triangles meet at the midpoint of the line that forms the dodecagon.
In this next example, you have another set of alternating major-minor chords. This one occurs between the first and second set contained in the previous example. It is similar to the second set in that the major triangles are connected to the minor triangles by their vertices. This set of triangles differ from the other three in that the vertices of the major-minor triangles meet at the midpoint of the line that forms the dodecagon.
I have more work I've done on this. I hope to be adding to this page as I have time.